正态分布的概率密度函数

作者：陈泽婉

文章来源：星火网校

最新编辑时间：1603346232

正态分布

　　正态分布，又名高斯分布，是高中数学学习的一个非常重要的概率分布，今天我们来学习的就是正态分布的概率密度函数。

　　正态分布的定义

　　
　　正态分布是一种概率分布，是具有两个参数μ和σ^2的连续型随机变量的分布，若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布，记为N(μ，σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。
　　

　　
　　服从正态分布的变量的频数分布由μ、σ完全决定。正态曲线呈钟型，两头低，中间高，左右对称因其曲线呈钟形，因此人们又经常称之为钟形曲线。正态分布具有以下特征：
　　
　　集中性：正态曲线的高峰位于正中央，即均数所在的位置；

对称性：正态曲线以均数为中心，左右对称，曲线两端永远不与横轴相交；

均匀变动性：正态曲线由均数所在处开始，分别向左右两侧逐渐均匀下降。
　　

　　
　　标准正态分布的概率密度函数为：

　　
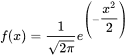
　　以上就是正态分布的概率密度函数及其相关知识点。正态分布在数学、物理及工程等领域都有应用，例如在医学上，群体的红细胞数、血红蛋白量呈现近似正态分布，根据此可以制定医学参考值范围，作为重要的指标。